8. Network robustness#
import networkx as nx
import seaborn as sns
8.1. Simulating random and targeted attacks to a network#
Resilience is the ability to provide and maintain an acceptable level of service in the face of faults and challenges to normal operation. Threats and challenges for services can range from simple misconfiguration over large scale natural disasters to targeted attacks.
We define a function that performs a random or targeted attack to a network according to a given strategy (random, degree based, betweenness based, etc. )
G = nx.Graph()
G.add_nodes_from([1, 2, 3, 4, 5, 6])
G.nodes
NodeView((1, 2, 3, 4, 5, 6))
from random import shuffle
lista = [1, 2, 3, 4, 5, 6]
shuffle(lista)
ranked_nodes = lista
ranked_nodes
[2, 3, 4, 5, 6, 1]
def net_attack(graph, ranked_nodes):
# here we store the tuples: (%removed nodes, size of gcc)
fraction_removed = []
graph1 = graph.copy()
nnodes = len(ranked_nodes)
n = 0
gcc = list(nx.connected_components(graph1))[0]
gcc_size = float(len(gcc)) / nnodes
fraction_removed.append((float(n) / nnodes, gcc_size))
while gcc_size > 0.01:
# we start from the end of the list!
graph1.remove_node(ranked_nodes.pop())
gcc = list(nx.connected_components(graph1))[0]
gcc_size = float(len(gcc)) / nnodes
n += 1
fraction_removed.append((float(n) / nnodes, gcc_size))
return fraction_removed
lista = [1, 2, 3, 4]
lista.pop()
4
8.2. Robustness of the US airport network#
8.2.1. Random attack#
filepath_air = "./../datasets/USairport_2010.txt"
G = nx.Graph()
fh = open(filepath_air, "r")
for line in fh.readlines():
s = line.strip().split()
G.add_edge(int(s[0]), int(s[1]))
fh.close()
airport_nodes = list(G.nodes())
print(G)
Graph with 405 nodes and 8251 edges
shuffle(lista)
resilience_random = net_attack(G, airport_nodes)
resilience_random
[(0.0, 0.9950617283950617),
(0.0024691358024691358, 0.9925925925925926),
(0.0049382716049382715, 0.9901234567901235),
(0.007407407407407408, 0.9876543209876543),
(0.009876543209876543, 0.9876543209876543),
(0.012345679012345678, 0.9876543209876543),
(0.014814814814814815, 0.9851851851851852),
(0.01728395061728395, 0.9827160493827161),
(0.019753086419753086, 0.980246913580247),
(0.022222222222222223, 0.9777777777777777),
(0.024691358024691357, 0.9753086419753086),
(0.027160493827160494, 0.9728395061728395),
(0.02962962962962963, 0.9703703703703703),
(0.03209876543209877, 0.9679012345679012),
(0.0345679012345679, 0.9654320987654321),
(0.037037037037037035, 0.9629629629629629),
(0.03950617283950617, 0.9604938271604938),
(0.04197530864197531, 0.9580246913580247),
(0.044444444444444446, 0.9555555555555556),
(0.04691358024691358, 0.9530864197530864),
(0.04938271604938271, 0.9506172839506173),
(0.05185185185185185, 0.9481481481481482),
(0.05432098765432099, 0.945679012345679),
(0.056790123456790124, 0.9432098765432099),
(0.05925925925925926, 0.9407407407407408),
(0.06172839506172839, 0.9382716049382716),
(0.06419753086419754, 0.9358024691358025),
(0.06666666666666667, 0.9333333333333333),
(0.0691358024691358, 0.9308641975308642),
(0.07160493827160494, 0.928395061728395),
(0.07407407407407407, 0.9259259259259259),
(0.07654320987654321, 0.9234567901234568),
(0.07901234567901234, 0.9209876543209876),
(0.08148148148148149, 0.9185185185185185),
(0.08395061728395062, 0.9160493827160494),
(0.08641975308641975, 0.9135802469135802),
(0.08888888888888889, 0.9111111111111111),
(0.09135802469135802, 0.908641975308642),
(0.09382716049382717, 0.9061728395061729),
(0.0962962962962963, 0.9037037037037037),
(0.09876543209876543, 0.9012345679012346),
(0.10123456790123457, 0.8987654320987655),
(0.1037037037037037, 0.8962962962962963),
(0.10617283950617284, 0.8938271604938272),
(0.10864197530864197, 0.891358024691358),
(0.1111111111111111, 0.8888888888888888),
(0.11358024691358025, 0.8864197530864197),
(0.11604938271604938, 0.8839506172839506),
(0.11851851851851852, 0.8814814814814815),
(0.12098765432098765, 0.8790123456790123),
(0.12345679012345678, 0.8765432098765432),
(0.1259259259259259, 0.8740740740740741),
(0.12839506172839507, 0.8716049382716049),
(0.1308641975308642, 0.8691358024691358),
(0.13333333333333333, 0.8666666666666667),
(0.13580246913580246, 0.8641975308641975),
(0.1382716049382716, 0.8617283950617284),
(0.14074074074074075, 0.8592592592592593),
(0.14320987654320988, 0.8567901234567902),
(0.145679012345679, 0.854320987654321),
(0.14814814814814814, 0.8518518518518519),
(0.1506172839506173, 0.8493827160493828),
(0.15308641975308643, 0.8469135802469135),
(0.15555555555555556, 0.8444444444444444),
(0.1580246913580247, 0.8419753086419753),
(0.16049382716049382, 0.8395061728395061),
(0.16296296296296298, 0.837037037037037),
(0.1654320987654321, 0.8345679012345679),
(0.16790123456790124, 0.8320987654320988),
(0.17037037037037037, 0.8296296296296296),
(0.1728395061728395, 0.8271604938271605),
(0.17530864197530865, 0.8246913580246914),
(0.17777777777777778, 0.8222222222222222),
(0.18024691358024691, 0.8197530864197531),
(0.18271604938271604, 0.817283950617284),
(0.18518518518518517, 0.8148148148148148),
(0.18765432098765433, 0.8123456790123457),
(0.19012345679012346, 0.8098765432098766),
(0.1925925925925926, 0.8074074074074075),
(0.19506172839506172, 0.8049382716049382),
(0.19753086419753085, 0.8024691358024691),
(0.2, 0.8),
(0.20246913580246914, 0.7975308641975308),
(0.20493827160493827, 0.7950617283950617),
(0.2074074074074074, 0.7925925925925926),
(0.20987654320987653, 0.7901234567901234),
(0.2123456790123457, 0.7876543209876543),
(0.21481481481481482, 0.7851851851851852),
(0.21728395061728395, 0.782716049382716),
(0.21975308641975308, 0.7802469135802469),
(0.2222222222222222, 0.7777777777777778),
(0.22469135802469137, 0.7753086419753087),
(0.2271604938271605, 0.7728395061728395),
(0.22962962962962963, 0.7703703703703704),
(0.23209876543209876, 0.7679012345679013),
(0.2345679012345679, 0.7654320987654321),
(0.23703703703703705, 0.762962962962963),
(0.23950617283950618, 0.7604938271604939),
(0.2419753086419753, 0.7580246913580246),
(0.24444444444444444, 0.7555555555555555),
(0.24691358024691357, 0.7530864197530864),
(0.24938271604938272, 0.7506172839506173),
(0.2518518518518518, 0.7481481481481481),
(0.254320987654321, 0.745679012345679),
(0.25679012345679014, 0.7432098765432099),
(0.25925925925925924, 0.7407407407407407),
(0.2617283950617284, 0.7382716049382716),
(0.2641975308641975, 0.7358024691358025),
(0.26666666666666666, 0.7333333333333333),
(0.2691358024691358, 0.7308641975308642),
(0.2716049382716049, 0.7283950617283951),
(0.2740740740740741, 0.725925925925926),
(0.2765432098765432, 0.7234567901234568),
(0.27901234567901234, 0.7209876543209877),
(0.2814814814814815, 0.7185185185185186),
(0.2839506172839506, 0.7160493827160493),
(0.28641975308641976, 0.7135802469135802),
(0.28888888888888886, 0.7111111111111111),
(0.291358024691358, 0.7086419753086419),
(0.2938271604938272, 0.7061728395061728),
(0.2962962962962963, 0.7037037037037037),
(0.29876543209876544, 0.7012345679012346),
(0.3012345679012346, 0.6987654320987654),
(0.3037037037037037, 0.6962962962962963),
(0.30617283950617286, 0.6938271604938272),
(0.30864197530864196, 0.691358024691358),
(0.3111111111111111, 0.6888888888888889),
(0.3135802469135803, 0.6864197530864198),
(0.3160493827160494, 0.6839506172839506),
(0.31851851851851853, 0.6814814814814815),
(0.32098765432098764, 0.6790123456790124),
(0.3234567901234568, 0.6765432098765433),
(0.32592592592592595, 0.674074074074074),
(0.32839506172839505, 0.671604938271605),
(0.3308641975308642, 0.6691358024691358),
(0.3333333333333333, 0.6666666666666666),
(0.3358024691358025, 0.6641975308641975),
(0.33827160493827163, 0.6617283950617284),
(0.34074074074074073, 0.6592592592592592),
(0.3432098765432099, 0.6567901234567901),
(0.345679012345679, 0.654320987654321),
(0.34814814814814815, 0.6518518518518519),
(0.3506172839506173, 0.6493827160493827),
(0.3530864197530864, 0.6469135802469136),
(0.35555555555555557, 0.6444444444444445),
(0.35802469135802467, 0.6419753086419753),
(0.36049382716049383, 0.6395061728395062),
(0.362962962962963, 0.6370370370370371),
(0.3654320987654321, 0.6345679012345679),
(0.36790123456790125, 0.6320987654320988),
(0.37037037037037035, 0.6296296296296297),
(0.3728395061728395, 0.6271604938271605),
(0.37530864197530867, 0.6246913580246913),
(0.37777777777777777, 0.6222222222222222),
(0.3802469135802469, 0.6197530864197531),
(0.38271604938271603, 0.6172839506172839),
(0.3851851851851852, 0.6148148148148148),
(0.38765432098765434, 0.6123456790123457),
(0.39012345679012345, 0.6098765432098765),
(0.3925925925925926, 0.6074074074074074),
(0.3950617283950617, 0.6049382716049383),
(0.39753086419753086, 0.6024691358024692),
(0.4, 0.6),
(0.4024691358024691, 0.5975308641975309),
(0.4049382716049383, 0.5950617283950618),
(0.4074074074074074, 0.5925925925925926),
(0.40987654320987654, 0.5901234567901235),
(0.4123456790123457, 0.5876543209876544),
(0.4148148148148148, 0.5851851851851851),
(0.41728395061728396, 0.582716049382716),
(0.41975308641975306, 0.5802469135802469),
(0.4222222222222222, 0.5777777777777777),
(0.4246913580246914, 0.5753086419753086),
(0.4271604938271605, 0.5728395061728395),
(0.42962962962962964, 0.5703703703703704),
(0.43209876543209874, 0.5679012345679012),
(0.4345679012345679, 0.5654320987654321),
(0.43703703703703706, 0.562962962962963),
(0.43950617283950616, 0.5604938271604938),
(0.4419753086419753, 0.5580246913580247),
(0.4444444444444444, 0.5555555555555556),
(0.4469135802469136, 0.5530864197530864),
(0.44938271604938274, 0.5506172839506173),
(0.45185185185185184, 0.5481481481481482),
(0.454320987654321, 0.5456790123456791),
(0.4567901234567901, 0.5432098765432098),
(0.45925925925925926, 0.5407407407407407),
(0.4617283950617284, 0.5382716049382716),
(0.4641975308641975, 0.5358024691358024),
(0.4666666666666667, 0.5333333333333333),
(0.4691358024691358, 0.5308641975308642),
(0.47160493827160493, 0.528395061728395),
(0.4740740740740741, 0.5259259259259259),
(0.4765432098765432, 0.5234567901234568),
(0.47901234567901235, 0.5209876543209877),
(0.48148148148148145, 0.5185185185185185),
(0.4839506172839506, 0.5160493827160494),
(0.48641975308641977, 0.5135802469135803),
(0.4888888888888889, 0.5111111111111111),
(0.49135802469135803, 0.508641975308642),
(0.49382716049382713, 0.5061728395061729),
(0.4962962962962963, 0.5037037037037037),
(0.49876543209876545, 0.5012345679012346),
(0.5012345679012346, 0.49876543209876545),
(0.5037037037037037, 0.4962962962962963),
(0.5061728395061729, 0.49382716049382713),
(0.508641975308642, 0.49135802469135803),
(0.5111111111111111, 0.4888888888888889),
(0.5135802469135803, 0.48641975308641977),
(0.5160493827160494, 0.4839506172839506),
(0.5185185185185185, 0.48148148148148145),
(0.5209876543209877, 0.47901234567901235),
(0.5234567901234568, 0.4765432098765432),
(0.5259259259259259, 0.4740740740740741),
(0.528395061728395, 0.47160493827160493),
(0.5308641975308642, 0.4691358024691358),
(0.5333333333333333, 0.4666666666666667),
(0.5358024691358024, 0.4641975308641975),
(0.5382716049382716, 0.4617283950617284),
(0.5407407407407407, 0.45925925925925926),
(0.5432098765432098, 0.4567901234567901),
(0.5456790123456791, 0.454320987654321),
(0.5481481481481482, 0.45185185185185184),
(0.5506172839506173, 0.44938271604938274),
(0.5530864197530864, 0.4469135802469136),
(0.5555555555555556, 0.4444444444444444),
(0.5580246913580247, 0.4419753086419753),
(0.5604938271604938, 0.43950617283950616),
(0.562962962962963, 0.43703703703703706),
(0.5654320987654321, 0.4345679012345679),
(0.5679012345679012, 0.43209876543209874),
(0.5703703703703704, 0.42962962962962964),
(0.5728395061728395, 0.4271604938271605),
(0.5753086419753086, 0.4246913580246914),
(0.5777777777777777, 0.4222222222222222),
(0.5802469135802469, 0.41975308641975306),
(0.582716049382716, 0.41728395061728396),
(0.5851851851851851, 0.4148148148148148),
(0.5876543209876544, 0.4123456790123457),
(0.5901234567901235, 0.40987654320987654),
(0.5925925925925926, 0.4074074074074074),
(0.5950617283950618, 0.4049382716049383),
(0.5975308641975309, 0.4024691358024691),
(0.6, 0.4),
(0.6024691358024692, 0.39753086419753086),
(0.6049382716049383, 0.3950617283950617),
(0.6074074074074074, 0.3925925925925926),
(0.6098765432098765, 0.39012345679012345),
(0.6123456790123457, 0.38765432098765434),
(0.6148148148148148, 0.3851851851851852),
(0.6172839506172839, 0.38271604938271603),
(0.6197530864197531, 0.3802469135802469),
(0.6222222222222222, 0.37777777777777777),
(0.6246913580246913, 0.37530864197530867),
(0.6271604938271605, 0.3728395061728395),
(0.6296296296296297, 0.37037037037037035),
(0.6320987654320988, 0.36790123456790125),
(0.6345679012345679, 0.3654320987654321),
(0.6370370370370371, 0.362962962962963),
(0.6395061728395062, 0.36049382716049383),
(0.6419753086419753, 0.35802469135802467),
(0.6444444444444445, 0.35555555555555557),
(0.6469135802469136, 0.3530864197530864),
(0.6493827160493827, 0.3506172839506173),
(0.6518518518518519, 0.34814814814814815),
(0.654320987654321, 0.345679012345679),
(0.6567901234567901, 0.3432098765432099),
(0.6592592592592592, 0.34074074074074073),
(0.6617283950617284, 0.33827160493827163),
(0.6641975308641975, 0.3358024691358025),
(0.6666666666666666, 0.3333333333333333),
(0.6691358024691358, 0.3308641975308642),
(0.671604938271605, 0.32839506172839505),
(0.674074074074074, 0.32592592592592595),
(0.6765432098765433, 0.3234567901234568),
(0.6790123456790124, 0.32098765432098764),
(0.6814814814814815, 0.31851851851851853),
(0.6839506172839506, 0.3160493827160494),
(0.6864197530864198, 0.3135802469135803),
(0.6888888888888889, 0.3111111111111111),
(0.691358024691358, 0.30864197530864196),
(0.6938271604938272, 0.30617283950617286),
(0.6962962962962963, 0.3037037037037037),
(0.6987654320987654, 0.3012345679012346),
(0.7012345679012346, 0.29876543209876544),
(0.7037037037037037, 0.2962962962962963),
(0.7061728395061728, 0.2938271604938272),
(0.7086419753086419, 0.291358024691358),
(0.7111111111111111, 0.28888888888888886),
(0.7135802469135802, 0.28641975308641976),
(0.7160493827160493, 0.2839506172839506),
(0.7185185185185186, 0.2814814814814815),
(0.7209876543209877, 0.27901234567901234),
(0.7234567901234568, 0.2765432098765432),
(0.725925925925926, 0.2740740740740741),
(0.7283950617283951, 0.2716049382716049),
(0.7308641975308642, 0.2691358024691358),
(0.7333333333333333, 0.26666666666666666),
(0.7358024691358025, 0.2641975308641975),
(0.7382716049382716, 0.2617283950617284),
(0.7407407407407407, 0.25925925925925924),
(0.7432098765432099, 0.25679012345679014),
(0.745679012345679, 0.254320987654321),
(0.7481481481481481, 0.2518518518518518),
(0.7506172839506173, 0.24938271604938272),
(0.7530864197530864, 0.24691358024691357),
(0.7555555555555555, 0.24444444444444444),
(0.7580246913580246, 0.2419753086419753),
(0.7604938271604939, 0.23950617283950618),
(0.762962962962963, 0.23703703703703705),
(0.7654320987654321, 0.2345679012345679),
(0.7679012345679013, 0.23209876543209876),
(0.7703703703703704, 0.22962962962962963),
(0.7728395061728395, 0.2271604938271605),
(0.7753086419753087, 0.22469135802469137),
(0.7777777777777778, 0.2222222222222222),
(0.7802469135802469, 0.21975308641975308),
(0.782716049382716, 0.21728395061728395),
(0.7851851851851852, 0.21481481481481482),
(0.7876543209876543, 0.2123456790123457),
(0.7901234567901234, 0.20987654320987653),
(0.7925925925925926, 0.2074074074074074),
(0.7950617283950617, 0.20493827160493827),
(0.7975308641975308, 0.20246913580246914),
(0.8, 0.2),
(0.8024691358024691, 0.19753086419753085),
(0.8049382716049382, 0.19506172839506172),
(0.8074074074074075, 0.1925925925925926),
(0.8098765432098766, 0.19012345679012346),
(0.8123456790123457, 0.18765432098765433),
(0.8148148148148148, 0.18518518518518517),
(0.817283950617284, 0.18271604938271604),
(0.8197530864197531, 0.18024691358024691),
(0.8222222222222222, 0.17777777777777778),
(0.8246913580246914, 0.17530864197530865),
(0.8271604938271605, 0.1728395061728395),
(0.8296296296296296, 0.17037037037037037),
(0.8320987654320988, 0.16790123456790124),
(0.8345679012345679, 0.1654320987654321),
(0.837037037037037, 0.16296296296296298),
(0.8395061728395061, 0.16049382716049382),
(0.8419753086419753, 0.1580246913580247),
(0.8444444444444444, 0.15555555555555556),
(0.8469135802469135, 0.15308641975308643),
(0.8493827160493828, 0.1506172839506173),
(0.8518518518518519, 0.14814814814814814),
(0.854320987654321, 0.145679012345679),
(0.8567901234567902, 0.14320987654320988),
(0.8592592592592593, 0.14074074074074075),
(0.8617283950617284, 0.1382716049382716),
(0.8641975308641975, 0.13580246913580246),
(0.8666666666666667, 0.13333333333333333),
(0.8691358024691358, 0.1308641975308642),
(0.8716049382716049, 0.12839506172839507),
(0.8740740740740741, 0.1259259259259259),
(0.8765432098765432, 0.12345679012345678),
(0.8790123456790123, 0.12098765432098765),
(0.8814814814814815, 0.11851851851851852),
(0.8839506172839506, 0.11604938271604938),
(0.8864197530864197, 0.11358024691358025),
(0.8888888888888888, 0.1111111111111111),
(0.891358024691358, 0.10864197530864197),
(0.8938271604938272, 0.10617283950617284),
(0.8962962962962963, 0.1037037037037037),
(0.8987654320987655, 0.10123456790123457),
(0.9012345679012346, 0.09876543209876543),
(0.9037037037037037, 0.0962962962962963),
(0.9061728395061729, 0.09382716049382717),
(0.908641975308642, 0.09135802469135802),
(0.9111111111111111, 0.08888888888888889),
(0.9135802469135802, 0.08641975308641975),
(0.9160493827160494, 0.08395061728395062),
(0.9185185185185185, 0.08148148148148149),
(0.9209876543209876, 0.07901234567901234),
(0.9234567901234568, 0.07654320987654321),
(0.9259259259259259, 0.07407407407407407),
(0.928395061728395, 0.07160493827160494),
(0.9308641975308642, 0.0691358024691358),
(0.9333333333333333, 0.06666666666666667),
(0.9358024691358025, 0.06419753086419754),
(0.9382716049382716, 0.06172839506172839),
(0.9407407407407408, 0.05925925925925926),
(0.9432098765432099, 0.056790123456790124),
(0.945679012345679, 0.05432098765432099),
(0.9481481481481482, 0.05185185185185185),
(0.9506172839506173, 0.04938271604938271),
(0.9530864197530864, 0.04691358024691358),
(0.9555555555555556, 0.044444444444444446),
(0.9580246913580247, 0.04197530864197531),
(0.9604938271604938, 0.03950617283950617),
(0.9629629629629629, 0.037037037037037035),
(0.9654320987654321, 0.0345679012345679),
(0.9679012345679012, 0.03209876543209877),
(0.9703703703703703, 0.02962962962962963),
(0.9728395061728395, 0.027160493827160494),
(0.9753086419753086, 0.024691358024691357),
(0.9777777777777777, 0.022222222222222223),
(0.980246913580247, 0.019753086419753086),
(0.9827160493827161, 0.01728395061728395),
(0.9851851851851852, 0.014814814814814815),
(0.9876543209876543, 0.012345679012345678),
(0.9901234567901235, 0.009876543209876543)]
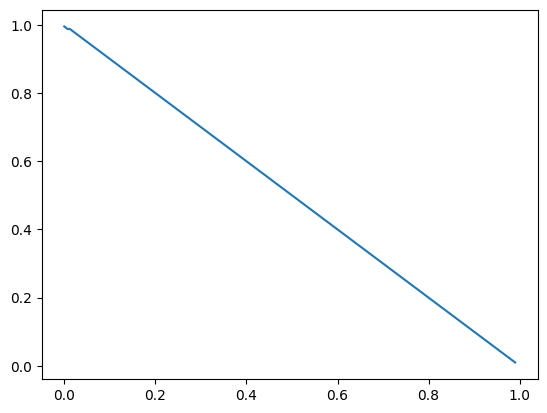
import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots()
data = np.array(resilience_random)
ax.plot(data[:, 0], data[:, 1])
[<matplotlib.lines.Line2D at 0x295ec0790>]
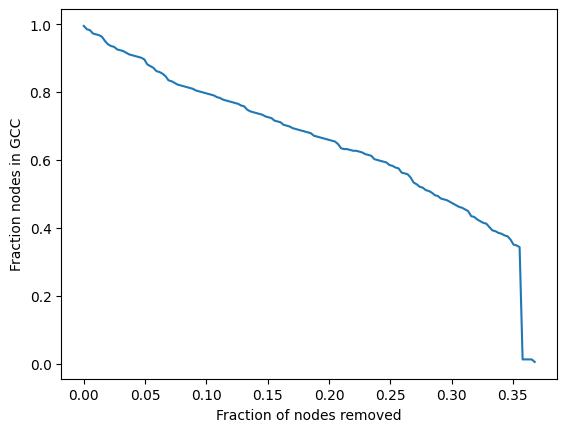
8.2.2. Betweenness based attack#
from operator import itemgetter
airport_nodes_betw = []
betw = nx.betweenness_centrality(G)
for i in sorted(betw.items(), key=itemgetter(1)):
airport_nodes_betw.append(i[0])
betw[389]
0.132272652064009
resilience_betw = net_attack(G, airport_nodes_betw)
fig, ax = plt.subplots()
data = np.array(resilience_betw)
ax.plot(data[:, 0], data[:, 1])
ax.set_ylabel("Fraction nodes in GCC")
ax.set_xlabel("Fraction of nodes removed")
Text(0.5, 0, 'Fraction of nodes removed')
8.2.3. Degree based attack#
airport_nodes_degree = []
deg = dict(G.degree())
for i in sorted(deg.items(), key=itemgetter(1)):
airport_nodes_degree.append(i[0])
resilience_deg = net_attack(G, list(airport_nodes_degree))
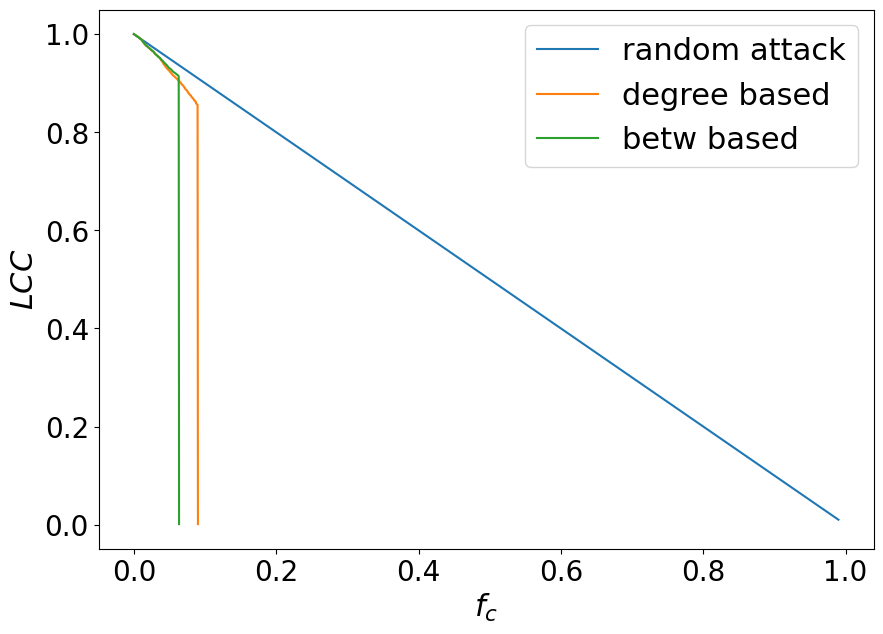
Let’s compare the results.
x = [k[0] for k in resilience_random]
y = [k[1] for k in resilience_random]
x1 = [k[0] for k in resilience_deg]
y1 = [k[1] for k in resilience_deg]
x2 = [k[0] for k in resilience_betw]
y2 = [k[1] for k in resilience_betw]
plt.figure(figsize=(10, 7))
plt.plot(x, y, label="random attack")
plt.plot(x1, y1, label="degree based")
plt.plot(x2, y2, label="betw based")
plt.xlabel("$f_{c}$", fontsize=22)
plt.ylabel("$LCC$", fontsize=22)
plt.xticks(fontsize=20)
plt.yticks(fontsize=22)
plt.legend(loc="upper right", fontsize=20)
<matplotlib.legend.Legend at 0x296571c70>
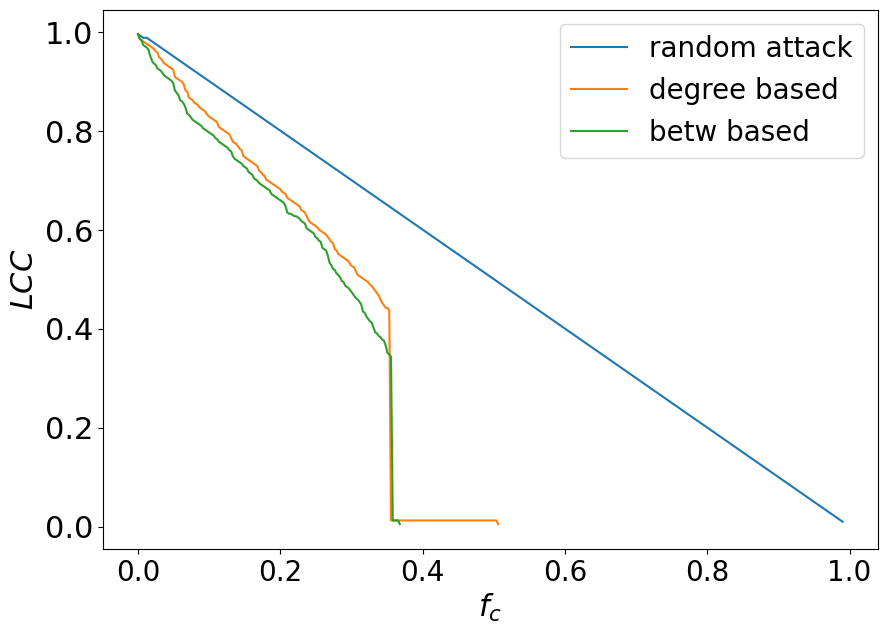
Real networks such as the air transport network are vulnerable to targeted attacks.
8.3. Robustness of the Erdos-Renyi random network#
ER = nx.fast_gnp_random_graph(2000, 0.012)
ER_nodes = list(ER.nodes())
# we rank the nodes by degree
ER_nodes_deg = [i for i, d in sorted(dict(ER.degree()).items(), key=itemgetter(1))]
ER_betw = nx.betweenness_centrality(ER)
ER_nodes_betw = [i for i, b in sorted(dict(ER_betw).items(), key=itemgetter(1))]
resilience_random = net_attack(ER, ER_nodes)
resilience_deg = net_attack(ER, ER_nodes_deg)
resilience_betw = net_attack(ER, ER_nodes_betw)
x = [k[0] for k in resilience_random]
y = [k[1] for k in resilience_random]
x1 = [k[0] for k in resilience_deg]
y1 = [k[1] for k in resilience_deg]
x2 = [k[0] for k in resilience_betw]
y2 = [k[1] for k in resilience_betw]
plt.figure(figsize=(10, 7))
plt.plot(x, y, label="random attack")
plt.plot(x1, y1, label="degree based")
plt.plot(x2, y2, label="betw based")
plt.xlabel("$f_{c}$", fontsize=22)
plt.ylabel("$LCC$", fontsize=22)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend(loc="upper right", fontsize=22)
<matplotlib.legend.Legend at 0x2966c8670>
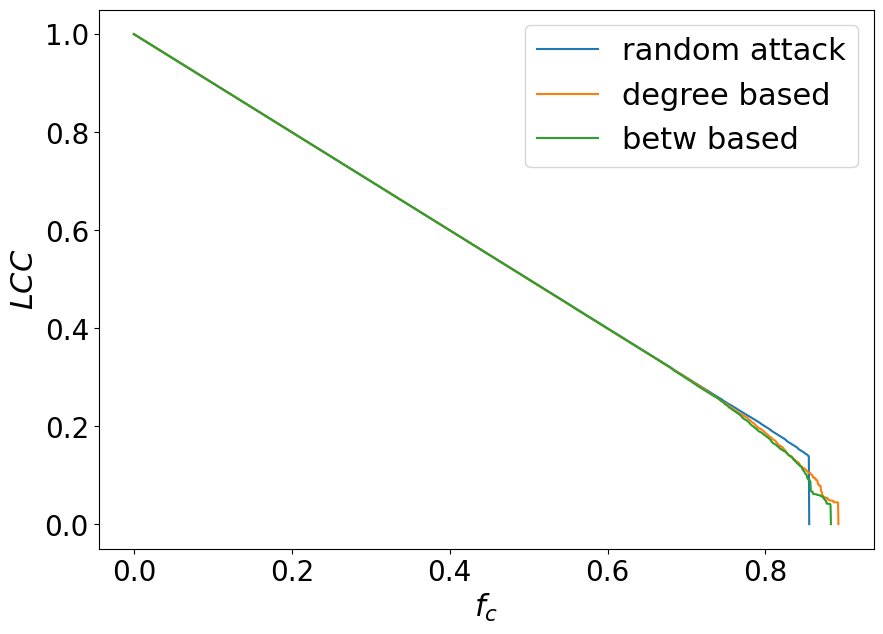
Random networks such as the E-R network are not vulnerable to targeted attacks.
8.4. Robustness of Barabasi-Albert network#
BA = nx.barabasi_albert_graph(2000, 3)
BA_nodes = list(BA.nodes())
# we rank the nodes by degree
BA_nodes_deg = [i for i, d in sorted(dict(BA.degree()).items(), key=itemgetter(1))]
BA_betw = nx.betweenness_centrality(BA)
BA_nodes_betw = [i for i, b in sorted(dict(BA_betw).items(), key=itemgetter(1))]
resilience_random = net_attack(BA, BA_nodes)
resilience_deg = net_attack(BA, BA_nodes_deg)
resilience_betw = net_attack(BA, BA_nodes_betw)
x = [k[0] for k in resilience_random]
y = [k[1] for k in resilience_random]
x1 = [k[0] for k in resilience_deg]
y1 = [k[1] for k in resilience_deg]
x2 = [k[0] for k in resilience_betw]
y2 = [k[1] for k in resilience_betw]
plt.figure(figsize=(10, 7))
plt.plot(x, y, label="random attack")
plt.plot(x1, y1, label="degree based")
plt.plot(x2, y2, label="betw based")
plt.xlabel("$f_{c}$", fontsize=22)
plt.ylabel("$LCC$", fontsize=22)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend(loc="upper right", fontsize=22)
<matplotlib.legend.Legend at 0x2982526a0>
from scipy.stats import zipf
a = 2.5
seq = zipf.rvs(a, loc=1, size=10000)
if np.sum(seq) % 2 != 0:
seq[0] = seq[0] + 1
gs = nx.configuration_model(seq[:2000])
# we rank the nodes by degree
gs_nodes = list(gs.nodes())
gs_nodes_deg = [i for i, d in sorted(dict(gs.degree()).items(), key=itemgetter(1))]
gs_betw = nx.betweenness_centrality(gs)
gs_nodes_betw = [i for i, b in sorted(dict(gs_betw).items(), key=itemgetter(1))]
---------------------------------------------------------------------------
NetworkXError Traceback (most recent call last)
Cell In [57], line 8
5 if np.sum(seq) % 2 != 0:
6 seq[0] = seq[0] + 1
----> 8 gs = nx.configuration_model(seq[:2000])
9 # we rank the nodes by degree
10 gs_nodes = list(gs.nodes())
File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/utils/decorators.py:845, in argmap.__call__.<locals>.func(_argmap__wrapper, *args, **kwargs)
844 def func(*args, __wrapper=None, **kwargs):
--> 845 return argmap._lazy_compile(__wrapper)(*args, **kwargs)
File <class 'networkx.utils.decorators.argmap'> compilation 28:4, in argmap_configuration_model_25(deg_sequence, create_using, seed)
2 import collections
3 import gzip
----> 4 import inspect
5 import itertools
6 import re
File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/generators/degree_seq.py:217, in configuration_model(deg_sequence, create_using, seed)
215 if sum(deg_sequence) % 2 != 0:
216 msg = "Invalid degree sequence: sum of degrees must be even, not odd"
--> 217 raise nx.NetworkXError(msg)
219 G = nx.empty_graph(0, create_using, default=nx.MultiGraph)
220 if G.is_directed():
NetworkXError: Invalid degree sequence: sum of degrees must be even, not odd
resilience_random = net_attack(gs, gs_nodes)
resilience_deg = net_attack(gs, gs_nodes_deg)
resilience_betw = net_attack(gs, gs_nodes_betw)
x = [k[0] for k in resilience_random]
y = [k[1] for k in resilience_random]
x1 = [k[0] for k in resilience_deg]
y1 = [k[1] for k in resilience_deg]
x2 = [k[0] for k in resilience_betw]
y2 = [k[1] for k in resilience_betw]
plt.figure(figsize=(10, 7))
plt.plot(x, y, label="random attack")
plt.plot(x1, y1, label="degree based")
plt.plot(x2, y2, label="betw based")
plt.xlabel("$f_{c}$", fontsize=22)
plt.ylabel("$LCC$", fontsize=22)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend(loc="upper right", fontsize=22)
<matplotlib.legend.Legend at 0x298a171f0>


